
Īcoustic positioning systems are the most used underwater external positioning approaches, from long baseline (LBL) to sort baseline (SBL) and ultrashort baseline (USBL).
For this reason, several works in the literature combine the information of proprioceptive sensors to external positioning systems. This fact makes unfeasible underwater dead-reckoning navigation. However, these proprioceptive sensors suffer from drift and biases, leading to growing position uncertainty as the vehicle navigates.

This is because the submerged vehicle cannot detect the electromagnetic signals provided by the global navigation satellite system (GNSS).

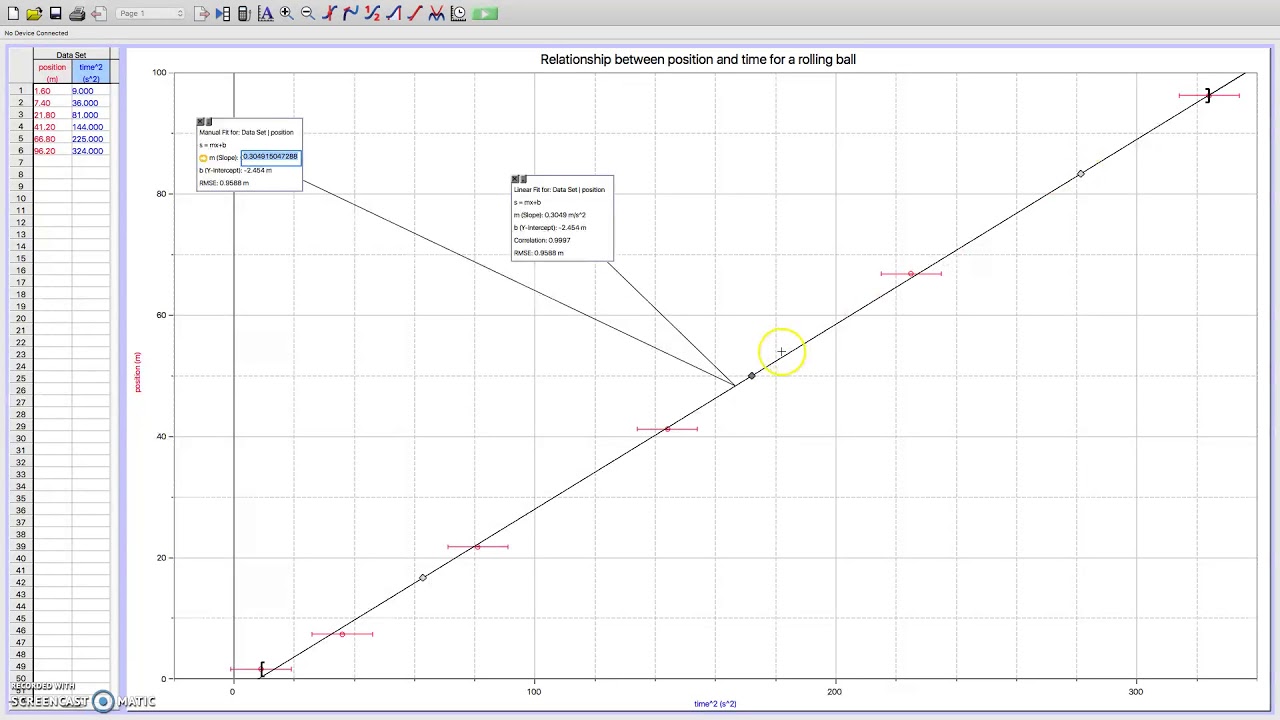
Underwater vehicles incorporating a certain degree of autonomy usually rely on proprioceptive sensors, such as an inertial navigation system (INS) integrated with Doppler velocity logs (DVLs). These vehicles can perform many tasks in a broad spectrum of applications, such as inspection, repair, and maintenance in defense, oil and gas, and cable surveying, to name but a few. Nowadays, underwater vehicles allow us access to restricted areas and traditionally dangerous environments for human divers, such as deep seabed and under the ice. Besides, they evaluate the improvement of localization compared to the position estimation using reliable dead-reckoning systems. The experimental results show that the framework provides a reliable environment representation during the underwater navigation to the localization system in real-world scenarios. We locate the underwater vehicle using a Sequential Monte Carlo (SMC) method initialized from the GPS location obtained on the surface. We evaluate the framework using cameras and range sensors for modeling uncertain features that represent the environment around the vehicle. By adopting uncertain modeling and multi-sensor fusion techniques, the framework can maintain a coherent representation of the environment, filtering outliers, inconsistencies in sequential observations, and useless information for positioning purposes. Submerged sensory information is often affected by diverse sources of uncertainty that can deteriorate the positioning and tracking. Hanging Mass (kg) | Spring Length (meters) | Stretch Distance, x (meters) | Stretching Force, F (N)Ġ.1 | 6.4cm/0.064m | 0.064-0.039=0.025m | 0.98NĠ.2 | 10.4cm/0.104m | 0.104-0.039=0.065m | 1.96NĠ.3 | 14.2cm/0.142m | 0.142-0.039=0.103m | 2.This paper presents a framework for processing, modeling, and fusing underwater sensor signals to provide a reliable perception for underwater localization in structured environments. Do not hang masses greater than 600 grams from the springs, or they may be permanently stretched out of shape. Important: The springs you are working with are quite delicate. The stretching force is just the weight (in Newtons) of the hanging mass. The stretch distance is the spring length minus the reading for zero added mass. Record your observations in the Table below.ģ. Choose a reference point somewhere near the bottom of the spring or masses from which to record the differences. Notice the resting position of the spring and record it first.Ģ. To determine the spring constant of the spring, hang masses from 100 to 600 grams, in 100-gram steps, on the spring. You can assume that the force applied on the spring by the hanging mass is proportional to the restoring force applied by the spring on the massĬalculation Ia: (1 pts) For each value of hanging mass on the spring, calculate the force applied 0n the spring:ġ. Question Ia: (1 pts) Based on your Graph 1a, can you conclude that the mass-spring system follows Hooke's law? Why or why not?Ĭalculation Ib: (2 pts) Using the slope of the linear regression in Graph 1a, calculate an experimental value for the spring constant and its uncertainty (using propagation oferror) for the conical spring: NB. Graph Ia: (3 pts) Using the data from Table 1 in the experimental details file and your Calc: 1a results, plot a graph of the position of the platform as a function of the force 'applied on the spring: Use the linear regression tool to fit your data and be sure to show the uncertainty ofyour linear fit parameters You should also show your data table in your graph file by using the "print" function in Logger Pro (and not "print graph") Be sure to give your graph an appropriate title that describes the data shown: SOLVED: Calculation Ia: (1 pts) For each value of hanging mass on the spring, calculate the force applied 0n the spring:


 0 kommentar(er)
0 kommentar(er)
